Note
Please see  https://doi.org/10.13140/RG.2.2.11927.69281
for the first draft of this series.
https://doi.org/10.13140/RG.2.2.11927.69281
for the first draft of this series.
The primary enhancements in this draft is the addition of a preliminary literature review, comments on clinical significance, non-parametric statistics, and neural networks.
Abstract
Conventional medicine treats laboratory tests as "within normal limits" or "abnormal," with no shades of grey in between. This paper explores the utility of using Z-scores to refine the diagnostic criteria for understanding the relationship between TSH (thyrotropin), T4, T3, fT4, fT3, and rT3 in the practice of functional and naturopathic medicine.
Conventional Medical View of Reference Ranges
The conventional medical view taught and practiced by allopathic MDs is based on the premise that any lab test result "within the reference range" supports the view that a patient is "normal" and disease-free and, therefore, not a candidate for treatment. On the other hand, any lab test result "outside the reference range" supports the patient being diagnosed with a disease that can be assigned an ICD-10 diagnosis code, and therefore, the patient becomes a candidate for treatment, and the treatment may be subject to third-party payer reimbursement.
This paper will unpack the statistical basis for this view in the following paragraphs. We must discuss certain statistical concepts, including the null hypothesis, statistical significance, confidence intervals, and Boolean logic to do this.
Null hypothesis
The null hypothesis is the starting point of statistical analysis. It states,
In order to make a diagnosis that a patient has a disease, the physician must show that the null hypothesis has a statistically significant probability of being wrong. Note the emphasis on probability rather than proof. Statistics cannot provide proof - only varying degrees of certitude.
There is no effect - there is no problem - prove me wrong.
Rejecting the null hypothesis
In order to diagnose the presence of disease in a patient, statistical evidence must be presented that "it is unlikely" that a healthy patient will present with the particular lab test. In this case, we reject the null hypothesis and accept the alternate hypothesis that there is sufficient statistical certainty that there is an effect, problem, or disease.
Statistical significance
When the statistical certitude that the null hypothesis can be rejected reaches a certain threshold, then it is said that there is statistically significant evidence that the alternative hypothesis (that the patient is diseased) should be accepted. Typically, in medicine, there must be a statistical certitude of at least 95% that the null hypothesis can be rejected for the alternate hypothesis that the patient has an effect, problem, or disease to be accepted. Put another way, there is less than 5% certitude that the patient is "normal." This certitude is often expressed as "having statistical significance at p = 0.05").
Clinical significance
Clinical significance differs from statistical significance. Whereas statistical significance says, "There is probably a measurable effect," clinical significance asks, "So what? Does this provide a meaningful benefit to the patient at a reasonably low cost and risk?" Determining clinical significance is a judgment call based on the value systems of the patient, doctor, and society, and it lies in the domain of medical ethics. For example, suppose a particular drug shows a statistically significant reduction in cardiovascular disease but must be taken for the rest of the patient's life, costs $100 a month, is associated with increased risk of liver disease, and on statistical average extends a patient's health-span by 1 month. What is the risk/benefit assessment of clinical significance for this drug?
Note that as the sample size of a statistical study increases, so does the power to find statistical significance for smaller and smaller effects. The smaller the effect, the less likely the treatment will be clinically significant. Also note that in some cases, a drug may have multiple adverse effects that are not statistically significant individually but are, in aggregate, both statistically and clinically significant. Thus, study end-points demonstrating reduced "all-cause" mortality are more clinically significant than end-points such as reduced "cardiovascular" mortality with non-statistically significant increases in liver disease, depression, etc.
Reference range
Various statistical techniques can estimate the reference range (the 95% confidence interval). The most straightforward approach is to collect 1,000 healthy individuals and run the lab test on them. Results are expected to vary according to random chance. If the 1,000 lab values are sorted from lowest to highest, and the 25 lowest and 25 highest values are discarded, then the range of the remaining values will represent the "middle" 95% of the sample. The lowest and highest remaining values represent an estimate of the reference range. This procedure only gives a statistical estimate based on a sample of 1,000 individuals. If the process were repeated with a new group of 1,000 healthy individuals, then a similar but not the same reference range is expected. A less repeatable reference range would be obtained if a smaller sample size were used (e.g., 200 healthy individuals and "trim" off the highest 5 values and the lowest 5 values). A larger sample size would give more repeatable results. The method described here is non-parametric, which means that it does not depend on any assumption of special properties of the data, such as "normal distribution" (see below). In practice, labs may base their reference ranges on statistical techniques that assume the data follows a normal distribution; these reference ranges are only reliable if the statistical assumptions made are valid. Regardless of how the reference range is obtained, it is treated as a uniform (rectangular) distribution in which any lab test value within the reference range equally satisfies the null hypothesis, and any value outside the reference range equally rejects the null hypothesis, which leads to all-or-nothing decision making, as described below.
Boolean logic
Boolean logic is a system of decision-making that is based on "true" and "false" with no intermediate "shades of gray." The conventional medical view taught and practiced by allopathic MDs uses Boolean logic to reason with test results. A given test result is classified as either "in the reference range," which means that it is FALSE that the patient has a problem, or "outside the reference range," which means that it is TRUE that the patient has a diagnosable problem. For example, if the reference range is 0.50 to 4.50, a patient with a test result of 0.51 is treated the same as a patient with a test result of 4.49 - i.e. is "within normal limits" and therefore has no disease diagnosis. The patient is put into a "box" 4 units wide. A smidge to the left or right would cause the patient to fall out of the box and be classified as "abnormally low" or "abnormally high." This view may cause patients near the edges of the box who would benefit from treatment to be told that they are "normal" and to be denied treatment.
Some researchers further recommend that "mild" elevations above the reference range may not be clinically significant. For example, [Onusko2008] states, "mild elevations of [ALT] or [AST] (<3 times the upper limit of normal [ULN]) following statin therapy do not appear to lead to significant liver toxicity over time ... routine monitoring of transaminases with statin therapy is not clinically necessary." Similarly, some researchers report that TSH levels up to 10mU/L may not be clinically significant for elderly patients [Garber2012 🕮 ] (the ULN is commonly regarded to be 4.5 mU/L).
Functional Medical View of Reference Ranges
One approach to improving on the conventional medical view as taught and practiced by allopathic MDs is to acknowledge that there are shades of gray between "true" and "false" so that a patient in the above example with lab values of 0.51, 2.5, and 4.4 would be classified as "low-normal," "mid-normal," and "high-normal," respectively. Clinical decision-making can, therefore, be more precise, but the rules for clinical decision-making become more complicated than the conventional approach.
One approach to this problem is introducing the idea of "fuzzy logic." While "fuzzy" may sound like a disdainful term, it acknowledges that decisions must be made with incomplete information of variable reliability in the real world. To implement fuzzy-logic decision-making, we can transform the patient's lab value into a Z-score in the same manner as is commonly done for DEXA scan reports of bone density. This Z-score can represent all shades of meaning from "low" (outside the reference range on the left) through "high" (outside the reference range on the right). To understand Z-scores, we must discuss certain statistical concepts, including the central limit theorem, population mean, standard deviation, and Z- transformation.
Central limit theorem
The distribution of many measured values subject to random independent variations tends to follow a "Gaussian," "normal," or "bell-shaped" distribution that approximates a binomial distribution. In particular, if the lab test results of many people are affected by random individual variation, then a graph of the values will be approximately normally distributed, and standard statistical techniques are applicable. In this view, the null hypothesis is most likely to be satisfied at the center of the "hump" of the bell curve and is progressively less likely to be satisfied as the patient's lab value moves left or right toward the "tails" of the bell curve.
This bell-shaped distribution assumption is not a perfect reflection of reality. However, it is a better approximation of reality than the uniform rectangular distribution implied by the conventional approach used by allopathic MDs as described above. As will be discussed below, fuzzy medical decision-making based on the assumption of a normal distribution of test results (e.g., statements like the patient's lab has a Z-score of -1, which means we are about 68% certain that the patient's lab value is abnormal) is expected to be more precise than Boolean medical decision-making using the "in the box/out of the box" approach of assuming a uniform rectangular distribution (which for that same patient we would say "the patient is normal)."
Population mean and standard deviation
Any Gaussian distribution curve can be characterized by the population mean (μ) and the standard deviation (σ). The population mean is the value that represents the top of the hump of the bell curve; the standard deviation is a measure of "how wide" the bell curve is. Without delving into all the mathematics, it can be shown that there is a simple approximate relationship between the reference range described in the conventional medical view and the population mean and standard deviation:
Let L and U represent the lower and upper bounds of the 95% reference range obtained as above (when applied to data that follows an approximately normal distribution).
Then the population mean = μ = (L+U)/2, and the standard deviation = σ = (U-L)/2 .
Z-scores
It is convenient to convert (transform) a patient's lab values into Z-scores.
The following formula converts the measured lab value (denoted V) to its corresponding Z-score (denoted Z):
Z = 2 * (V - μ) / σ
These transformed values have the following convenient properties according to the 68-95 rule:
- Z = 0 means that the patient's lab value is in the middle of the reference range and is most likely normal (the patient is normal from an allopathic perspective);
- Z < -2 means that the patient's lab value is lower than the 95% reference range - reject the null hypothesis at a level of p=0.05 (we are more than 95% certain the patient has a diagnosable disorder from an allopathic perspective);
- Any Z value between -2 and +2 lies within the 95% reference range (within 2 standard deviations of the middle) - accept the null hypothesis at a level of p=0.05 (we are less than 95% certain the patient has a diagnosable disorder, so the patient is considered normal from an allopathic perspective);
- Z > +2 means that the patient's lab value is greater than the 95% reference range - reject the null hypothesis at a level of p=0.05 (we are more than 95% certain the patient has a diagnosable disorder from an allopathic perspective);
- Z-scores are real numbers with a continuum of values representing shades of gray (naturopathic and functional medical perspective) - not just true or false (allopathic medical perspective).
Extending the power of Z-Scores
An advantage of Z-scores is that the reference range is always from -2 to +2, so it is easy to tell where a lab value lies relative to the reference range (low, normal, high). Even more powerful, since Z-scores are continuous, degrees of belief in the null hypothesis can be expressed by intermediate values. If we assume that the test data is approximately normally distributed (which follows from the Central Limit Theorem of statistics), then given the 95% upper and lower bounds of the test data (L and U) and the patient's test value (V), then we can calculate a Z value as follows. For example, consider the case of TSH (reference range = 0.45 to 4.5) and a measured lab value = 3.5, as follows:
Example:
L = 0.5, U = 4.5, and V = 3.5; then
Z = 2 * (V - ?) / ? = 2 * (3.5 - 2.5) / 2 = +1.0
I.e., the patient's lab value is 1 standard deviation higher than the mid-range.Based on the 68-95 rule, we are 68% certain the null hypothesis can be rejected, which means we are 68% certain the patient has a problem that deserves intervention. Do we wait until we are more than 95% certain the patient has a problem, or do we begin mild interventions sooner rather than wait for the patient to cross the line into 95% certainty of abnormality? Where do we draw the line between intervention and watchful waiting?
Assumptions
The following assumptions are more or less accurate - they are not perfect. However, their usefulness is highlighted by a short story:
The story's moral is that the analysis presented here better approximates reality than conventional allopathic medicine, even if imperfect. Therefore, we expect a better, if not perfect, patient response to treatment.
Two hikers in the woods encountered a bear, which began to chase them. As they ran, the first hiker gasped, It is no use - we cannot outrun the bear! To which the second hiker grunted, I do not have to outrun the bear - I only have to outrun you!
Normality assumption
Standard parametric statistical methods depend on the assumption that the probability density function (PDF) is normal (Gaussian).
In the case of TSH [Fontes2013 🕮 ] reports that the
 Kolmogorov-Smirnov Test
shows the PDF of TSH to be non-Gaussian (lognormal) (exhibits kurtosis [Blanca2013]) but can be transformed
into an approximately Gaussian distribution using a logarithmic transformation.
The Kolmogorov-Smirnov Test is a non-parametric test that can determine whether two sample data sets came from the
same probability distribution.
The logarithmic transformation has been criticized by [Feng2014 🕮 ], [Feng2019 🕮 ], and
Kolmogorov-Smirnov Test
shows the PDF of TSH to be non-Gaussian (lognormal) (exhibits kurtosis [Blanca2013]) but can be transformed
into an approximately Gaussian distribution using a logarithmic transformation.
The Kolmogorov-Smirnov Test is a non-parametric test that can determine whether two sample data sets came from the
same probability distribution.
The logarithmic transformation has been criticized by [Feng2014 🕮 ], [Feng2019 🕮 ], and
 ResearchGate.
ResearchGate.
In the case of freeT4, [Fontes2013 🕮 ] reports that freeT4 exhibits a Gaussian distribution.
Further literature research (or access to appropriate raw data) is necessary to clarify the PDF of the remaining thyroid analytes. The biggest problem is that raw data is generally unavailable to determine the shape of the PDFs. Presumably, the labs providing the tests have the required data, which they used to establish their reference ranges. However, can we find labs willing to share this information?
Optimality assumption
In the absence of any specific information to the contrary, we assume that the optimal value for a lab value is the center of the reference range, where Z = 0. In other words, the center of "normal" = "optimal." For example, in the thyroid system, a patient is in optimum balance when Z(TSH) = Z(T4) = Z(fT4) = Z(T3) = Z(fT3) = Z(rT3) = 0.
Causation assumption
- It is assumed that at each step of the pathway TSH → T4 → T3 + reverseT3,
there is a causative correlation between the titer of the precursor and product.
This assumption has been confirmed by [Fontes2013 🕮 ] in a healthy population for the case of TSH → freeT4,
where the authors report a "high level of significance" inverse correlation between log10(TSH) and fT4 using the Pearson correlation
coefficient test, which showed an r-value between -0.3862 and -0.4946.
However, [Johansen1978 🕮 ] reports that in a hypothyroid population the serum TSH or log10(TSH) vs freeT4 and freeT3 showed a nonlinear inverse relationship.
[Ryder1980 🕮 ] reports that TSH correlates better with T4 than T3.
Similarly, [Kahn1978 🕮 ] reports a better reciprocal correlation between TSH and T4 than between TSH and T3.
Dr. Weyrich is not surprised since he expects that the TSH → T4 and T4 → T3 correlations are imperfect due to different confounding factors, so the TSH → T3 correlation should be doubly imperfect. - [Kahn1978 🕮 ] reports that various patterns of T4 and T3 are associated with elevated TSH:
- normal T4 and normal T3 (19.5%);
- low T4 and elevated T3 (8%);
- low T4 and normal T3 (37%);
- low T4 and low T3 (35.5%).
Likewise, [Kumar1977 🕮 ] concludes that "T4 and T3 may function together to maintain euthyroidism, and that in addition to serum TSH, T4 ... has more diagnostic value than ... T3." - [Ferrari1987 🕮 ] reports that TSH has a significant inverse correlation with freeT4, T4/TBG ratio, T4, and freeT3 in hypothyroid patients,
but freeT4 is the variable that discriminates best between control subjects and hypothyroid patients.
Similarly, [Kahn1978 🕮 ] reports a better reciprocal correlation between TSH and T4 than between TSH and T3. - [Erfurth1986 🕮 ] observes that the mean ratio between T3 and T4 in euthyroid subjects was less than in hypothyroid subjects,
independent of TSH levels.
This observation suggests some mechanism preserving T4 better than T3 in primary thyroid failure. Dr. Weyrich suggests that this reinforces the finding of [Erfurth1986 🕮 ] that freeT4 is a stronger indicator of hypothyroid status than TSH or freeT3. - [Pekary1980 🕮 ] reports that an inverse linear relationship between TSH and T4 or T3 is found for individuals when
TSH levels are manipulated.
When a collection of individual trend lines is averaged, the result is the "familiar hyperbolic relationship between thyrotrophin
and thyroid hormone levels."
Dr. Weyrich notes that this is an important finding, which suggests that when confounding factors are constant within an individual, the transfer functions between TSH → T4 and T4 → T3 are linear. - [Aizawa1978 🕮 ] notes a correlation between the size of the sella turcica and the severity of a patient's hypothyroid condition. Dr. Weyrich presumes that this correlation is mediated by increased hypothalamic release of TRH, which drives the pituitary to produce more TSH.
- [Bemben1994 🕮 ] reviewed 283 elderly patients with no previous history of thyroid disease and found that 15% of these patients exhibited
subclinical hypothyroidism, which they defined as elevated TSH levels of 5.0 to 14.9 mU/L and normal free T4 levels of 0.7 to 2.0 ng/dL.
By these criteria, they found no significant differences in the frequencies of any of the clinical signs and symptoms of hypothyroidism
between euthyroid and hypothyroid patients.
They concluded that "thyroid status could not be predicted from clinical signs and symptoms in this sample of elderly community-dwelling patients."
Dr. Weyrich counters that an alternative conclusion is that the TSH and T4 criteria used fail to explain the clinical signs and symptoms of hypothyroidism and the criteria should be reconsidered.
Confounding factors
Dr. Weyrich notes that a perfect inverse correlation would have r = -1, which suggests that there are also significant confounding factors affecting the correlation between log10(TSH) and freeT4, which may include:
- [Fontes2013 🕮 ] reports that TSH increases very significantly with age, while fT4 slightly decreases with age.
[Carle2007 🕮 ] reports similar findings.
Dr. Weyrich notes that this suggests that the negative feedback loop between the thyroid and the pituitary is mostly successful in maintaining homeostasis (compensation) of fT4 despite the apparent age-related loss of thyroid function. A competing hypothesis is that with increasing age, the hypothalamus/pituitary becomes more active, which causes the thyroid gland to down-regulate to maintain homeostasis, which appears less likely to Dr. Weyrich. In other words, in most cases, thyroid function appears to be the independent variable, rather than pituitary function, which reacts to negative feedback. - [Alevizaki2005 🕮 ] notes an inverse correlation between TSH and SHBG and also reports the
"slopes of the regression lines of T3 to TSH were significantly different in the control group and the hypothyroid group:
thus, for the same TSH levels, T3 levels were lower in the hypothyroid group.
This observation argues that using TSH levels to monitor T4 replacement therapy may be misleading as a measure of adequate levels of thyroid hormone in tissues such as the liver because intracellular T3 status in the pituitary [due to the action of DIO2] may not reflect the T3 status in the periphery [due to the action of DIO1]. - Iodine nutritional status [Shahid2025].
[Philippou1992 🕮 ] reports that the daily administration of 150 mg of potassium iodide to hyperthyroid patients caused T4, T3, and reverseT3 to decrease and thyroxine-binding globulin to increase. Trends were smaller and less predictable for euthyroid and hypothyroid patients.
[Waldhausl1976 🕮 ] reports that the administration of 25 mg iodide (daily for 2 weeks) to euthyroid patients reduced T4 and T3 levels. - Increased estrogen levels can increase binding proteins and thereby increase the ratio of T4 to freeT4 (assuming compensatory negative feedback increases TSH) [Shahid2025].
- TSH receptor antibodies (Graves disease) [Shahid2025].
- Antibodies to thyroid peroxidase or thyroglobulin (Hashimoto thyroiditis) [Shahid2025].
- Ectopic production of thyroid hormone in some conditions, leading to increased thyroid hormones and compensatory TSH decrease [Shahid2025].
- High doses of biotin supplementation interfere with the immunoassay tests for TSH, resulting in suppressed lab value (but not affecting the physiology of the thyroid system itself) [Ardabilygazir2018 🕮 ].
- [Kahana1983 🕮 ] has observed a decrease in TSH in a group of high cortisol patients versus low cortisol patients under the stress
of an acute myocardial infarction.
However, [Sinha2023 🕮 ], [Walter2012 🕮 ], [Abdulateef2019 🕮 ] report a positive correlation between TSH and cortisol. - [Borst1983 🕮 ] reports that fasting or poor caloric intake in the critically ill can lower TSH and mask hypothyroid states.
However, [Shulkin1985 🕮 ] reports that "caloric restriction in both untreated and T4-treated hypothyroid patients is accompanied by ... reduced serum T3 concentrations, as it is euthyroid subjects, and ... no alterations in ... TSH secretion." - [Yamauchi1984 🕮 ] suggests, "Systolic time intervals (ET/PEP) can discriminate between euthyroid and hyperthyroid states. ... T4 doses [should be] adjusted to maintain normal ET/PEP rather than normal serum TSH levels, especially in older patients in whom T4 may aggravate angina pectoris or provoke myocardial infarction." Systolic time intervals can be measured using pulsed Doppler echocardiography [Boudoulas1990 🕮 ]. See also [Nuutila1992 🕮 ].
- [Chaudhary2023 🕮 ] reports an inverse correlation between thyroid density evaluated by Computed Tomography and TSH.
Factors that can affect conversion of T4 → T3 and T4 → reverseT3 include:
- The enzymes DIO1 (in the liver and kidney) and DIO2 (in the central nervous system, pituitary, brown adipose tissue, and muscle) convert T4 → T3 [Peeters2017].
- Genetic deficiency of DIO2 causes central resistance to exogenous T4, which is characterized by elevated TSH that is not responsive to administration of exogenous T4 [Lacamara2020 🕮 ].
- The enzyme DIO3 (in the brain) converts T4 → rT3 and T3 → 3,3'-T2 [Peeters2017].
- The enzyme DIO1 also degrades rT3 → 3,3'-T2 [Peeters2017].
- T4 is also metabolized by (phase II detoxification) sulfation and glucuronidation [Peeters2017].
- The iodothyronine sulfates and glucuronides are excreted in the bile. They can be hydrolyzed back to iodothyronines by bacterial β-glucuronidases and bacterial sulfatases in the intestines and then reabsorbed (enterohepatic recirculation) [Peeters2017]. This process may be modulated by gut dysbiosis.
- The iodothyronine deiodinases DIO1, DIO2, and DIO3 all contain selenoproteins at their active site, so selenium nutritional deficiency impairs the production of T4, T3, etc. [Peeters2017].
- In non-thyroidal illness (NTI) and malnutrition/extreme dieting, plasma T3 often decreases, and plasma rT3 increases
[Peeters2017].
Similarly, [Wadwekar2004 🕮 ] reports that during acute illness, "Serum T4, T3 declined to a nadir and serum rT3 rose to its peak by day 3 of hospitalization before returning to pre-admission euthyroid levels. Serum TSH declined initially but rose to supernormal levels on day 7 before normalization."
[Tibaldi1985 🕮 ] suggests that "because the changes in thyroid hormone metabolism that occur in non-thyroidal disease probably represent adaptive changes to the illness, treatment with L-thyroxine to restore serum thyroid concentrations to the normal range is not indicated."
[Mahashabde2024 🕮 ] refers to this condition as Sick Euthyroid Syndrome (SES), which commonly occurs in critically ill patients, such as heart failure, chronic kidney disease, and severe sepsis. Typically, these patients present with low T3 and normal or low levels of thyroxine T4 and TSH. As discussed by [Tibaldi1985 🕮 ], SES appears to be an adaptive response to reduce the body's metabolic rate. - Drugs, including propylthiouracil, dexamethasone, propranolol, iodinated radiographic contrast, and amiodarone, inhibit the various iodothyronine deiodinases by several mechanisms [Peeters2017].
- Genetic variations in deiodinase activity have been reported, as well as variations in the SECIS-binding protein SBP2, which is required for the synthesis of the selenoproteins found in iodothyronine deiodinases [Bianco2019 🕮 ].
- Zinc or copper deficiencies are associated with reduced production of T4. Paradoxically, thyroid hormone is required for the absorption of zinc. Furthermore, zinc is required for the T3 receptor to function [Betsy2013 🕮 ], [Maxwell2007 🕮 ].
- Iron deficiency anemia has been associated with decreased thyroperoxidase activity, reduced T4 and T3 production, and increased reverseT3 production. The mechanism is unclear [Soliman2017 🕮 ].
- High doses of biotin supplementation interfere with the immunoassay tests for T4 and T3, resulting in elevated lab values (but not affecting the physiology of the thyroid system itself) [Ardabilygazir2018 🕮 ]
- In a rat model, [Helmreich2011 🕮 ] reports that stress was associated with decreases in peripheral TSH, T4, and T3 but not reverseT3. Dr. Weyrich notes that this implies that the reverseT3 / T3 ratio was increased.
- [Kahana1983 🕮 ] has observed a decrease in T3 and an increase in rT3 in a group of high cortisol patients
versus low cortisol patients under the stress of acute myocardial infarction.
[Sinha2023 🕮 ] reports a negative correlation between serum T4 and T3 levels and serum cortisol in hypothyroidism.
[Khandelwal2012 🕮 ] states that hypocortisolism must be addressed prior to initiating T4/T3 replacement therapy. - A study of COVID-19-infected outpatients had significantly lower serum T3 but higher T4 than non-infected participants
[Naghashpour2022 🕮 ].
Another study reported that adrenal insufficiency, low T3, low TSH, and hyperprolactinemia were common in COVID-19 hospitalized patients. "hsCRP showed a rising trend with disease severity while IL-6 did not" [Kumar2021 🕮 ]. - [Inada1980 🕮 ] showed that administering exogenous T3 can reduce reverseT3.
- [Douyon2002 🕮 ] States that less than 10% of obese individuals are hypothyroid, but overfeeding may increase T3 and decrease reverseT3. On the other hand, hypocaloric diets decrease T4, T3, freeT3 and increase reverseT3 (resembling sick euthyroid syndrome).
- High cortisol levels can raise reverseT3 levels and block the conversion of T4 into T3 [need cite]. They are also associated with decreased TSH and free T4 [Cai2020 🕮 ].
- Stress can also cause the body to convert more T4 into reverseT3 instead of T3. This conversion is often a protective mechanism to prevent the body from going into overdrive. Inflammation may also be associated with elevated reverseT3 [need cite].
- Liver conditions like non-alcoholic fatty liver disease can sometimes increase T4 to T3 conversion as a compensatory mechanism, but generally, liver problems can decrease this conversion [Leo; need cite].
Conversion proportionality assumption
In the absence of any specific information to the contrary, we assume that for a process in which one precursor is converted through one or more steps to a product, if the conversion pathway proceeds at a normal rate, then the Z value of the precursor should be proportional to the Z value of the product. Note that if Z(precursor) > Z(product), it may imply either an abnormally active subsequent step is siphoning off the product or the conversion is impaired. For example, in the thyroid pathway, Z(T4) should equal Z(T3) and also equal Z(rT3) in the case of "normal rate of conversion."
Control inverse proportionality assumption
In the absence of any specific information to the contrary, we assume that if a product exerts a negative feedback loop that suppresses the production of a control substance, the Z(control) should be inversely proportional to the Z(product). This is in the case of Z(TSH) and Z(T4).
Applications
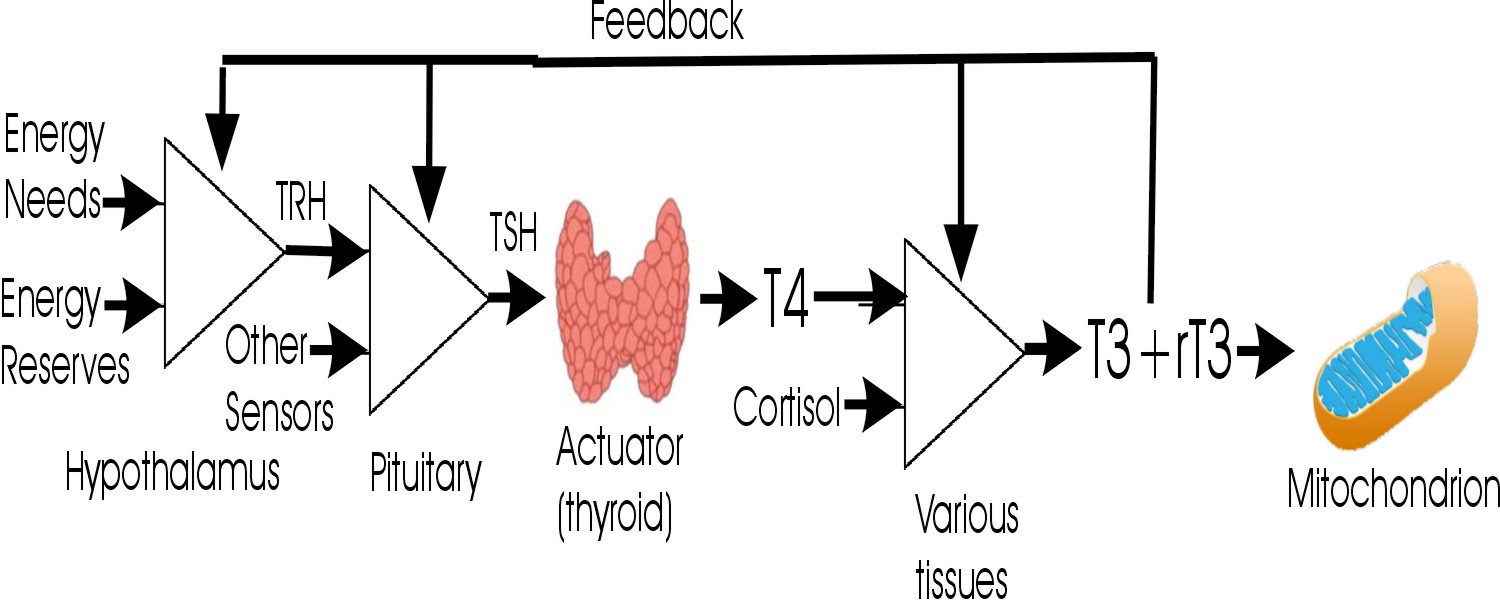
See more details  here
here
Consider the thyroid metabolic pathway below, with Z-values for lab tests. Note that since there is an inverse correlation between log(TSH) and T4, we place a negative sign in front of Z(log(TSH)).
-Z(log(TSH)) = +3
Z(T4) = +1
Z(T3) = -3
Z(rT3) = 0
This patient is hypothyroid, but why?
All three of these issues need to be addressed in the treatment plan.
- -Z(log(TSH)) > Z(T4), so we suspect the thyroid gland is underperforming.
- Z(T4) > Z(T3), so we suspect that conversion from T4 to T3 is underperforming.
- Z(T3) < Z(rT3), so we suspect the rT3 pathway dominates rather than the T3 pathway.
Now consider:
-Z(log(TSH)) = -1.9
Z(T4) = -1.5
Z(T3) = -1.5
Z(rT3) = +1.9
By conventional standards, this patient is euthyroid but has clinical symptoms. Why?
In this case, we need to reduce rT3 by supplementing with exogenous T3 or nutritional support for the endogenous conversion of T4 to T3 (e.g., selenium and other micronutrients).
- -Z(log(TSH)) < Z(T4), so there is no evidence that the thyroid gland is underperforming - it is not being stimulated.
- Z(T4) = Z(T3), so there is no evidence of a problem converting T4 to T3.
- Z(T3) << Z(rT3), so we suspect that the rT3 pathway is dominating rather than the T3 pathway.
- Z(TSH) << Z(rT3), so we suspect that rT3 is suppressing TSH via negative feedback.
Extension to Fuzzy Logic and Probabilistic Reasoning
Since a Z score of ±1 corresponds to a 68% probability that there is an effect (the null hypothesis fails), and a Z score of ±2 corresponds to a 95% probability that there is an effect (the null hypothesis fails), we can extend our reasoning to propose that if the difference between two Z scores (e.g. Z(TSH) and Z(T4)) equals 1, then there is a 68% probability (P) that the difference is statistically significant. Similarly, if the difference equals 2, there is a 95% probability (P) that the difference is statistically significant.
Boolean logic is used in the conventional medical view of reference ranges to reduce clinical decision-making as to whether it is true or false that each lab value is within the reference range. The functional medical view of reference ranges allows the comparison of non-binary values of different lab parameters using Z-scores. While this is an improvement, it suffers from the limitation that while Z-scores Z(a) and Z(b) can be compared to establish that Z(a) is less than, equal, or greater than Z(b), the significance of the comparison is not defined.
The next step in the development of the theory of thyroid statistics is to develop statistical functions that convert comparisons of Z values into probability functions. For example, if Z(a) = -1 and Z(b) = +0.5, what is the probability that Z(a) < Z(b)? What is the probability that Z(a) = Z(b)? What is the probability that Z(a) > Z(b)? What is the probability that Z(a) is less than the reference range? What is the probability that Z(a) exceeds the reference range? These probabilities are non-zero, but some are much smaller than others.
Based on the assumption that our reference range has a normal distribution, standard statistical calculations should allow all of these functions to be developed using the Excel function NORMSDIST function, which calculates the Standard Normal Cumulative Distribution Function for a supplied value.
Extension to Non-parametric (Robust) Statistical Analysis
Since some probability distribution functions are either unknown or known to be non-Gaussian, consideration should be given to reframing the analysis in terms of non-parametric statistical methods.
Extension to Neural Nets
Given the number of confounding factors identified above, as well as the ill-defined probability distributions and covariances, the application of neural nets and Machine Learning (not Large Language Models) might also be a fruitful approach to diagnosing various endocrine disruptions involving the Hypothalamic-Pituitary-Thyroid-Cortisol axis.
This paper is a Draft for Public Comment
Please send comments and constructive feedback to orville2@DrWeyrich.com
The most current version of this paper is available at
 https://drweyrich.com/multimedia-archive/20250102-Thyroid%20Statistics.html
https://drweyrich.com/multimedia-archive/20250102-Thyroid%20Statistics.html
Help wanted!
I need access to anonymized thyroid lab data for TSH, F4, T3, freeT4, freeT3, and reverseT3, which is suitable for determining reference ranges, mean, and standard deviation, and evaluating possible deviations from normality. Is anyone having access to such data open to collaborating with me?
Going a step further, it would be even better for me to get access to paired data records containing data for multiple parameters for each (anonymous) individual, possibly including limited demographic data such as sex, age, nutritional sataus, and possibly week of pregnancy in order to evaluate correlations.
References
Links to Wikipedia are controversial, but when provided above, Dr. Weyrich has evaluated the content and believes that they are accurate and the most convenient sources unencumbered by copyrights or paywalls.






